Coseno

En un triángulo rectángulo, es la longitud del lado adyacente dividida por la longitud de la hipotenusa. La abreviación es cos. Ejemplo: en un triángulo con lados de 3, 4 y 5, el coseno del ángulo donde se encuentran los lados de longitud 4 y 5 es 4/5.

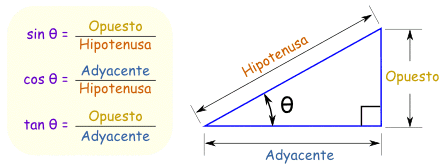
El coseno de un ángulo α de un triángulo rectángulo se define como la razónentre el cateto contiguo (b) y la hipotenusa (c). Su abreviatura es cos (del latín cosinus). Coseno de ángulos característicos El coseno de los ángulos más característicos es: Características del coseno Dominio:  Recorrido:  Derivada de la función coseno:  Integral de la función coseno:  Representación gráfica de la función coseno La función del coseno es periódica de período 360º (2π radianes), por lo que esta sección de la gráfica se repetirá en los diferentes períodos. Representación geométrica del coseno Relaciones del coseno con las restantes razones trigonométricas Relación del coseno con el seno: Relación del coseno con la tangente: Relación del coseno con la cosecante: Relación del coseno con la secante: Relación del coseno con la cotangente: (1) Nota: el signo que corresponde en cada caso depende del cuadrante en que esté el ángulo. Coseno del ángulo complementario, suplementario, conjugado y opuesto Coseno del ángulo complementario: Coseno del ángulo suplementario: Coseno del ángulo conjugado: Coseno del ángulo opuesto: Coseno de ángulos que difieren 90º: Coseno de ángulos que difieren 180º: Coseno del ángulo suma, resta, doble y mitad Coseno del ángulo suma: Coseno del ángulo resta: Coseno del ángulo doble: Coseno del ángulo mitad: Coseno del ángulo triple: Transformaciones de razones trigonométricas Transformación de razones trigonométricas de suma en producto Transformación de razones trigonométricas de producto en suma fuentes: http://www.universoformulas.com/matematicas/trigonometria/coseno/